Evidencia de actividad de ley de ohm
Conductor
No Conductor

- 2)
Circuito RL-serie
 Un circuito RL es un circuito eléctrico que contiene una resistencia y una bobina en serie. Se dice que la bobina se opone transitoriamente al establecimiento de una corriente en el circuito.
Un circuito RL es un circuito eléctrico que contiene una resistencia y una bobina en serie. Se dice que la bobina se opone transitoriamente al establecimiento de una corriente en el circuito.La ecuación diferencial que rige el circuito es la siguiente:
Circuito RL en serie.

Donde:
 es la tensión en los bornes de montaje, en V;
es la tensión en los bornes de montaje, en V;  es la intensidad de corriente eléctrica en A;
es la intensidad de corriente eléctrica en A;  es la inductancia de la bobina en H;
es la inductancia de la bobina en H;  es la resistencia total del circuito en Ω.
es la resistencia total del circuito en Ω.circito RL paralelo
El circuito en estudio, se denomina R-L, debido a que esta formado por resistencias y un inductor. El
comportamiento del inductor en un circuito dificulta que se presenten cambios rápidos en la corriente, debido a los
efectos de la fem autoinducida.
La caída de voltaje en un inductor es:
dt
di(t) VL (t) = L (1)
La misma muestra que cuanto mayor sea la razón de cambio de corriente di/dt, mayor será la diferencia
de potencial entre los terminales del inductor.
Los resistores en el circuito tienen la función de disipar la energía del mismo en forma de calor. La caída
de voltaje en un resistor es:
V (t) R i(t) R = ⋅ (2)
Estas ecuaciones junto con las reglas de Kirchoff, dan los principios para analizar el circuito en estudio.
Utilizando las reglas de Kirc
circuito RC serie
Un circuito RC es un circuito compuesto de resistencias y condensadores alimentados por una fuente eléctrica. Un circuito RC de primer orden está compuesto de un resistor y un condensador y es la forma más simple de un circuito RC. Los circuitos RC pueden usarse para filtrar una señal, al bloquear ciertas frecuencias y dejar pasar otras. Los filtros RC más comunes son el filtro paso alto, filtro paso bajo, filtro paso banda, y el filtro elimina banda. Entre las características de los circuitos RC está la propiedad de ser sistemas lineales e invariantes en el tiempo; reciben el nombre de filtros debido a que son capaces de filtrar señales eléctricas de acuerdo a su frecuencia.
En la configuración de paso bajo la señal de salida del circuito se coge en bornes del condensador, estando este conectado en serie con la resistencia. En cambio en la configuración de paso alto la tensión de salida es la caída de tensión en la resistencia.
circuito RLC serie
Si un circuito RLC en serie es sometido a un escalón de tensión 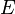 , la ley de las mallas impone la relación:
, la ley de las mallas impone la relación:
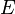 , la ley de las mallas impone la relación:
, la ley de las mallas impone la relación:
Introduciendo la relación característica de un condensador:
Se obtiene la ecuación diferencial de segundo orden:
Donde:
- E es la fuerza electromotriz de un generador, en Voltios (V);
- uC es la tensión en los bornes de un condensador, en Voltios (V);
- L es la inductancia de la bobina, en Henrios (H);
- i es la intensidad de corriente eléctrica en el circuito, en Amperios (A);
- q es la carga eléctrica del condensador, en Coulombs (C);
- C es la capacidad eléctrica del condensador, en Faradios (F);
- Rt es la resistencia total del circuito, en Ohmios (Ω);
- t es el tiempo en segundos (s)
En el caso de un régimen sin pérdidas, esto es para  , se obtiene una solución de la forma:
, se obtiene una solución de la forma:
 , se obtiene una solución de la forma:
, se obtiene una solución de la forma:

- circuito RLC paralelo

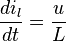
 ya que
ya que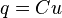

 Atención, la rama C es un corto-circuito:de esta manera no se pueden unir las ramas A y B directamente a los bornes de un generador E, se les debe adjuntar una resistencia.Las dos condiciones iniciales son:
Atención, la rama C es un corto-circuito:de esta manera no se pueden unir las ramas A y B directamente a los bornes de un generador E, se les debe adjuntar una resistencia.Las dos condiciones iniciales son: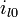 conserva su valor antes de la puesta en tensión (porque la inductancia se opone a la variación de corriente).
conserva su valor antes de la puesta en tensión (porque la inductancia se opone a la variación de corriente). conserva su valor antes de la puesta en tensión
conserva su valor antes de la puesta en tensión  .
.
- caracteristicas de la corriente alterna
- frecuencia
- La frecuencia tiene una relación inversa con el concepto de longitud de onda (ver gráfico), a mayor frecuencia menor longitud de onda y viceversa. La frecuencia f es igual a la velocidad v de la onda, dividido por la longitud de onda λ (lambda):Cuando las ondas viajan de un medio a otro, como por ejemplo de aire a agua, la frecuencia de la onda se mantiene constante, cambiando sólo su longitud de onda y la velocidad.Por el efecto Doppler, la frecuencia es una magnitud invariable en el universo. Es decir, no se puede modificar por ningún proceso físico excepto por su velocidad de propagación o longitud de onda.
- periodo
Tiempo necesario para que un ciclo se repita. Se mide en segundos y se representa con la letra P.
Frecuencia y periodo son valores inversos
T =1/f f =1/T

amplitud
- En una onda transversal, corresponde a la distancia máxima que se puede separar una
- partícula del medio que oscila, medida en forma perpendicular a la línea que representa la
- posición de equilibrio del medio. Se mide en unidades de longitud, preferentemente el
- metro (m).

- Importante: La amplitud de una onda representa la energía que transporta una onda. La
- energía y la amplitud, en este caso, son cantidades directamente proporcionales
LONGITUD DE ONDA
La longitud de onda representa la distancia existente entre dos picos o crestas consecutivos, dos valles consecutivos o el doble de la distancia entre un nodo y otro de la onda sinusoidal o senoidal de una corriente alterna, medida en metros. La longitud de onda se representa por medio de la letra griega lambda (
 ).
).De acuerdo con la longitud que posea una onda sinusoidal, además del metro como unidad de medida, se utilizan también múltiplos, como el kilómetro (km) y submúltiplos como el centímetro (cm), el milímetro (mm) y el nanómetro (nm) (un nanómetro equivale a la millonésima parte de un metro = 10-9metros = 0,000000001 m).
La longitud de una onda sinusoidal es inversamente proporcional a la frecuencia de la corriente. Es decir, a frecuencias muy bajas la onda puede alcanzar kilómetros de longitud entre cresta y cresta, mientras que a frecuencias más altas la distancia se acorta.
La frecuencia de la corriente que suministran los generadores o alternadores de las plantas eléctricas a las industrias y ciudades es, por ejemplo, de 50 ciclos por segundo o hertz (Hz) en Europa y de 60 ciclos por segundo o hertz en América. Para generar corrientes de 50 ciclos de frecuencia, los generadores tienen que girar a una velocidad constante de 3000 min-1 (revoluciones por minuto, o rpm) Si dividimos 3000 min-1 entre 60 segundos obtendremos como resultado 50 ciclos. Por otra parte, para obtener 60 Hz de frecuencia es necesario aumentar la velocidad de giro del rotor del generador o alternador hasta alcanzar 3600 rpm (3600 min-1 / 60 seg = 60 ciclos).
La unidad de medida de la corriente alterna se denomina hertz (Hz), en honor del físico alemán Heindrich Rudolf Hertz (1857 – 1894), quien descubrió el principio que rige la propagación de las ondas electromagnéticas, conocidas también como “ondas hertzianas”. Años más tarde el físico e inventor italiano Guglielmo Marconi, basándose en ese principio descubierto por Hertz, logró construir el primer transmisor de ondas de radio.
La frecuencia de la corriente alterna para uso industrial y doméstico ocupa sólo una pequeña porción del espectro de ondas electromagnéticas, correspondiente a las frecuencias extremadamente bajas, mientras que las de radio, televisión, microondas, rayos infrarrojos, etc., alcanzan valores de frecuencias mucho más altos.
ciclo
EL CICLO:Es la variación completa de la tensión o la corriente de cero a un valor máximo positivo y luego de nuevo a cero y de este a un valor máximo negativo y finalmente a cero.
fase
FASE: Es la fracción de ciclo transcurrido desde el inicio del mismo, su símbolo es la letra griega q.Período: Es el tiempo que tarda en producirse un ciclo de C.A. completo se denomina T. En nuestro ejemplo de una tensión de 220 V 50 Hz su período es de 20 mseg.La relación entre la frecuencia y el período es F=1/T
desfase
Es el ángulo que define la posición de una senoidal respecto a otra. Para averiguar el desfase hay que determinarlo en un punto de referencia de las senoidales; elegimos el punto donde pasan por 0 con pendiente positiva (subiendo). El desfase puede ser en retraso o en adelanto.







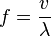
No hay comentarios:
Publicar un comentario